LSTM network introduction

RNN （recurrent neural network)

         LSTM (long short term memory) 是一種RNN network。RNN是一種可以記憶的神經網路，一般傳統的神經網路或是CNN（ convolution neural network)，神經元的資訊完全由當下輸入data貢獻，但某些問題像是語音辨識、語言翻譯，除了當下輸入的data，之前的data 也同樣重要。例如"I grew up in France…I speak fluent French "，假設後一個字"French"未知，我們可從前面"speak" 推測是某種語言，又從前文"grew up in France" 可推測為"French"，因此前文的資訊是非常重要的。
          為了讓神經元保有前面的記憶，RNN神經元除了與當下輸入的data 連接，還跟過去的神經元連接，如下圖所示

出處：https://read01.com/N6n3Ba.html

Xt 是時間 t 輸入，A為神經網路，ht 為時間t 輸出。可以看到，網路A除了X貢獻，還從過去的網路貢獻，以此達到記憶的功能。

LSTM (long short term memory) 

       然而傳統的RNN 當連接的網路愈久遠，backpropagation 時的gradient 愈小，學習效果愈差（gradient vanish)，也就是太久之前的記憶傳統RNN 很難學習。LSTM 就是來解決這個問題。傳統的RNN如下，與過去神經元連接只有一個tanh層運算

出處：https://read01.com/N6n3Ba.html

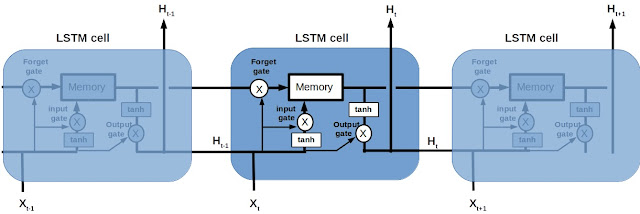
LSTM 就比較複雜了，示意圖如下，X 為input data，H 為output。

LSTM裡有一個memory 記憶區，不像傳統RNN 完全輸入完全輸出，而是有3個 gate控制這個memory 的更新及輸出 "input gate、output gate、forget gate"。
Forget gate 決定前一個Cell 的memory 有多少要丟到新cell 的memory 裡
Input gate   決定有多少新資料資訊要進入memory （新資料包含目前的input data Xt + 前面的output Ht-1)
Output gate 決定更新後的memory 有多少資訊要輸出LSTM cell 到下一層network

gate 是由Xt 及 前面output Ht-1決定，model 為線性分類器，以forget gate 為例子，數學式如下:

ft : forget gate，一維矩陣。因為sigmoid function的作用，gate 內的元素範圍介於 0~1。New memory 是 old memory 乘上 forget gate (element-wise) 的結果。當gate元素為0，old memory 不輸入new memory。gate 為1，old memory 完全移植到new memory。gate介於 0~1，部分輸入new memory。因此gate 內的元素決定了一定比例的old memory 要被忘記(0:全忘記，1: 全記住)，才稱作forget gate。然後 Wxf、Whf、b 都是可訓練的參數，經過訓練後，forget gate 就可依輸入的Xt 及Ht-1，正確的決定old memory 該忘記那些，該忘記多少，來對未來做更好的預測。
input gate、output gate 數學形式完全一樣，只是有各自的weights 跟 bias。

it : input gate. ot:output gate

gt是實際要輸入進memory 的新資訊，要進入多少由input gate 決定。

Tensorflow 實現

Udacity deep learning 的習題 assignment 6 介紹了LSTM 如何使用。習題內容是訓練一個model，輸入一串英文字母，讓model預測下一個英文字母為何，code 如下:

from __future__ import print_function
import os
import numpy as np
import random
import string
import tensorflow as tf
import zipfile
from six.moves import range
from six.moves.urllib.request import urlretrieve

url = 'http://mattmahoney.net/dc/'

def maybe_download(filename, expected_bytes):
  """Download a file if not present, and make sure it's the right size."""
  if not os.path.exists(filename):
    filename, _ = urlretrieve(url + filename, filename)
  statinfo = os.stat(filename)
  if statinfo.st_size == expected_bytes:
    print('Found and verified %s' % filename)
  else:
    print(statinfo.st_size)
    raise Exception(
      'Failed to verify ' + filename + '. Can you get to it with a browser?')
  return filename

filename = maybe_download('text8.zip', 31344016)

#Utility functions to map characters to vocabulary IDs and back.
def read_data(filename):
  with zipfile.ZipFile(filename) as f:
    name = f.namelist()[0]
    data = tf.compat.as_str(f.read(name))
  return data
  
text = read_data(filename)
print('Data size %d' % len(text))

valid_size = 1000
valid_text = text[:valid_size]
train_text = text[valid_size:]
train_size = len(train_text)
print(train_size, train_text[:64])
print(valid_size, valid_text[:64])

vocabulary_size = len(string.ascii_lowercase) + 1 # [a-z] + ' '
first_letter = ord(string.ascii_lowercase[0])

def char2id(char):
  if char in string.ascii_lowercase:
    return ord(char) - first_letter + 1
  elif char == ' ':
    return 0
  else:
    print('Unexpected character: %s' % char)
    return 0
  
def id2char(dictid):
  if dictid > 0:
    return chr(dictid + first_letter - 1)
  else:
    return ' '

print(char2id('a'), char2id('z'), char2id(' '), char2id('ï'))
print(id2char(1), id2char(26), id2char(0))

batch_size=64
num_unrollings=10

class BatchGenerator(object):
  def __init__(self, text, batch_size, num_unrollings):
    self._text = text
    self._text_size = len(text)
    self._batch_size = batch_size
    self._num_unrollings = num_unrollings
    segment = self._text_size // batch_size
    self._cursor = [ offset * segment for offset in range(batch_size)]
    self._last_batch = self._next_batch()
  
  def _next_batch(self):
    """Generate a single batch from the current cursor position in the data."""
    batch = np.zeros(shape=(self._batch_size, vocabulary_size), dtype=np.float)
    for b in range(self._batch_size):
      batch[b, char2id(self._text[self._cursor[b]])] = 1.0
      self._cursor[b] = (self._cursor[b] + 1) % self._text_size
    return batch
  
  def next(self):
    """Generate the next array of batches from the data. The array consists of
    the last batch of the previous array, followed by num_unrollings new ones.
    """
    batches = [self._last_batch]
    for step in range(self._num_unrollings):
      batches.append(self._next_batch())
    self._last_batch = batches[-1]
    return batches
def characters(probabilities):
  """Turn a 1-hot encoding or a probability distribution over the possible
  characters back into its (most likely) character representation."""
  return [id2char(c) for c in np.argmax(probabilities, 1)]

def batches2string(batches):
  """Convert a sequence of batches back into their (most likely) string
  representation."""
  s = [''] * batches[0].shape[0]
  for b in batches:
    s = [''.join(x) for x in zip(s, characters(b))]
  return s

train_batches = BatchGenerator(train_text, batch_size, num_unrollings)
valid_batches = BatchGenerator(valid_text, 1, 1)
print (train_text[0:30])
print (valid_text[0:30])
print(batches2string(train_batches.next()))
print(batches2string(train_batches.next()))
print(batches2string(valid_batches.next()))
print(batches2string(valid_batches.next()))

def logprob(predictions, labels):
  """Log-probability of the true labels in a predicted batch."""
  predictions[predictions < 1e-10] = 1e-10 #why need smaller than 1e-10
  return np.sum(np.multiply(labels, -np.log(predictions))) / labels.shape[0] #why log need * -1 

def sample_distribution(distribution):
  """Sample one element from a distribution assumed to be an array of normalized
  probabilities.
  """
  r = random.uniform(0, 1)
  s = 0
  for i in range(len(distribution)):
    s += distribution[i]
    if s >= r:
      return i
  return len(distribution) - 1

def sample(prediction):
  """Turn a (column) prediction into 1-hot encoded samples."""
  p = np.zeros(shape=[1, vocabulary_size], dtype=np.float)
  p[0, sample_distribution(prediction[0])] = 1.0
  return p

def random_distribution():
  """Generate a random column of probabilities."""
  b = np.random.uniform(0.0, 1.0, size=[1, vocabulary_size])
  return b/np.sum(b, 1)[:,None]

num_nodes = 64

graph = tf.Graph()
with graph.as_default():
  
  # Parameters:
  # Input gate: input, previous output, and bias.
  ix = tf.Variable(tf.truncated_normal([vocabulary_size, num_nodes], -0.1, 0.1))
  im = tf.Variable(tf.truncated_normal([num_nodes, num_nodes], -0.1, 0.1))
  ib = tf.Variable(tf.zeros([1, num_nodes]))
  # Forget gate: input, previous output, and bias.
  fx = tf.Variable(tf.truncated_normal([vocabulary_size, num_nodes], -0.1, 0.1))
  fm = tf.Variable(tf.truncated_normal([num_nodes, num_nodes], -0.1, 0.1))
  fb = tf.Variable(tf.zeros([1, num_nodes]))
  # Memory cell: input, state and bias.                             
  cx = tf.Variable(tf.truncated_normal([vocabulary_size, num_nodes], -0.1, 0.1))
  cm = tf.Variable(tf.truncated_normal([num_nodes, num_nodes], -0.1, 0.1))
  cb = tf.Variable(tf.zeros([1, num_nodes]))
  # Output gate: input, previous output, and bias.
  ox = tf.Variable(tf.truncated_normal([vocabulary_size, num_nodes], -0.1, 0.1))
  om = tf.Variable(tf.truncated_normal([num_nodes, num_nodes], -0.1, 0.1))
  ob = tf.Variable(tf.zeros([1, num_nodes]))
  # Variables saving state across unrollings.
  saved_output = tf.Variable(tf.zeros([batch_size, num_nodes]), trainable=False)
  saved_state = tf.Variable(tf.zeros([batch_size, num_nodes]), trainable=False)
  # Classifier weights and biases.
  w = tf.Variable(tf.truncated_normal([num_nodes, vocabulary_size], -0.1, 0.1))
  b = tf.Variable(tf.zeros([vocabulary_size]))
  # Definition of the cell computation.
  def lstm_cell(i, o, state):
    """Create a LSTM cell. See e.g.: http://arxiv.org/pdf/1402.1128v1.pdf
    Note that in this formulation, we omit the various connections between the
    previous state and the gates."""
    input_gate = tf.sigmoid(tf.matmul(i, ix) + tf.matmul(o, im) + ib)
    forget_gate = tf.sigmoid(tf.matmul(i, fx) + tf.matmul(o, fm) + fb)
    update = tf.matmul(i, cx) + tf.matmul(o, cm) + cb
    state = forget_gate * state + input_gate * tf.tanh(update)
    output_gate = tf.sigmoid(tf.matmul(i, ox) + tf.matmul(o, om) + ob)
    return output_gate * tf.tanh(state), state

  # Input data.
  train_data = list()
  for _ in range(num_unrollings + 1):
    train_data.append(
      tf.placeholder(tf.float32, shape=[batch_size,vocabulary_size]))
  train_inputs = train_data[:num_unrollings]
  train_labels = train_data[1:]  # labels are inputs shifted by one time step.
  
  # Unrolled LSTM loop.
  outputs = list()
  output = saved_output
  state = saved_state
  
  for i in train_inputs:
    output, state = lstm_cell(i, output, state)#why don`t use output as varable directly ?? 
    outputs.append(output)
    
  # State saving across unrollings.
    
  
 
  
  with tf.control_dependencies([saved_output.assign(output),
                               saved_state.assign(state)]): #to save output & state in saved_output&saved_state
    # Classifier.
      test0 = saved_output
      test1 = output
      logits = tf.nn.xw_plus_b(tf.concat(outputs, 0), w, b)#tf.concat let list of tensor become a tesnor
      loss = tf.reduce_mean(
          tf.nn.softmax_cross_entropy_with_logits(
            labels=tf.concat(train_labels, 0), logits=logits))
  
  
      
  # Optimizer.
  global_step = tf.Variable(0)
  learning_rate = tf.train.exponential_decay(
    10.0, global_step, 5000, 0.1, staircase=True)
  optimizer = tf.train.GradientDescentOptimizer(learning_rate)   
  gradients, v = zip(*optimizer.compute_gradients(loss)) #split gradient and variable
  gradients, _ = tf.clip_by_global_norm(gradients, 1.25) #control gradient to avoid gradients vanishing
  optimizer = optimizer.apply_gradients(
    zip(gradients, v), global_step=global_step)

  # Predictions.
  train_prediction = tf.nn.softmax(logits)
  #print ( train_prediction )
  # Sampling and validation eval: batch 1, no unrolling.
  sample_input = tf.placeholder(tf.float32, shape=[1, vocabulary_size])
  saved_sample_output = tf.Variable(tf.zeros([1, num_nodes]))
  saved_sample_state = tf.Variable(tf.zeros([1, num_nodes]))
  reset_sample_state = tf.group(
    saved_sample_output.assign(tf.zeros([1, num_nodes])),
    saved_sample_state.assign(tf.zeros([1, num_nodes])))
  sample_output, sample_state = lstm_cell(
    sample_input, saved_sample_output, saved_sample_state)
  with tf.control_dependencies([saved_sample_output.assign(sample_output),
                                saved_sample_state.assign(sample_state)]):
    sample_prediction = tf.nn.softmax(tf.nn.xw_plus_b(sample_output, w, b))

num_steps = 20000
summary_frequency = 100

with tf.Session(graph=graph) as session:
  tf.global_variables_initializer().run()
  print('Initialized')
  mean_loss = 0
  for step in range(num_steps):
    batches = train_batches.next()
    feed_dict = dict()
    for i in range(num_unrollings + 1):
      feed_dict[train_data[i]] = batches[i]
    _, l, predictions, lr = session.run(
      [optimizer, loss, train_prediction, learning_rate], feed_dict=feed_dict)
    mean_loss += l
    
    if step % summary_frequency == 0:
      if step > 0:
        mean_loss = mean_loss / summary_frequency
      # The mean loss is an estimate of the loss over the last few batches.
      print(
        'Average loss at step %d: %f learning rate: %f' % (step, mean_loss, lr))
      mean_loss = 0
      labels = np.concatenate(list(batches)[1:])
      
      print('Minibatch perplexity: %.2f' % float(
        np.exp(logprob(predictions, labels))))
      if step % (summary_frequency * 10) == 0:
        # Generate some samples.
        print('=' * 80)
        for _ in range(5):
          feed = sample(random_distribution())
          sentence = characters(feed)[0]
          reset_sample_state.run()
          for _ in range(79):
            prediction = sample_prediction.eval({sample_input: feed})
            feed = sample(prediction)
            sentence += characters(feed)[0]
          print(sentence)
        print('=' * 80)
      # Measure validation set perplexity.
      reset_sample_state.run()
      valid_logprob = 0
      for _ in range(valid_size):
        b = valid_batches.next()
        predictions = sample_prediction.eval({sample_input: b[0]})
        valid_logprob = valid_logprob + logprob(predictions, b[1])
      print('Validation set perplexity: %.2f' % float(np.exp(
        valid_logprob / valid_size)))

LSTM cell 的實現為這幾行:

def lstm_cell(i, o, state):
    """Create a LSTM cell. See e.g.: http://arxiv.org/pdf/1402.1128v1.pdf
    Note that in this formulation, we omit the various connections between the
    previous state and the gates."""
    input_gate = tf.sigmoid(tf.matmul(i, ix) + tf.matmul(o, im) + ib)
    forget_gate = tf.sigmoid(tf.matmul(i, fx) + tf.matmul(o, fm) + fb)
    update = tf.matmul(i, cx) + tf.matmul(o, cm) + cb
    state = forget_gate * state + input_gate * tf.tanh(update)
    output_gate = tf.sigmoid(tf.matmul(i, ox) + tf.matmul(o, om) + ob)
    return output_gate * tf.tanh(state), state

update 是要輸入memory 的新資料，實際輸入 =  tf.tanh(update)*input_gate
state 就是儲存的 memory
output = output_gate * tf.tanh(state)


在training 時，變數state (memory) 跟 output (output of LSTM cell) 是必須存起來，給下一個training step 使用，tensorflow 是利用 tf.control_dependencies 來完成

with tf.control_dependencies([saved_output.assign(output),
                               saved_state.assign(state)]):

將output, state assign 到saved_output, saved_state 中存起來，但這段code 的使用我還不太懂，無法重複實現其他的code。

Perplexity

training 時的 cost，是以 perplexity 來表達，與一般圖形分類直接使用cross entropy 的總和不一樣。perplexity 的值代表有多少選擇，值等於2 表示預測時只有兩種選擇，5 就代表有五種選擇，所以值越大可選擇的越多，代表model 預測很不一定，當然錯誤率就越高，表示cost 越大。

結果預測

Model 在預測時，以往圖形分類都是用最後一層的softmax 輸出，直接取值最大的種類
當預測結果，但這邊卻是將softmax 輸出當機率分布然後取樣，取樣到的種類當結果，雖然值越大的種類取樣機率越高，但不是100%。也就是softmax 值最大的種類，有可能不被選中當作預測結果! 為何要用取樣而不是直接取機率最大，原因我還不懂.........